Asymptotic Notations

Asymptotic notations are used to represent the complexities of algorithms for asymptotic analysis. These notations are mathematical tools to represent the complexities. There are three notations that are commonly used.

• Big Oh Notation
• Big Omega Notation
• Big Theta Notation

Big Oh Notation

Big-Oh (O) notation gives an upper bound for a function f(n) to within a constant factor.

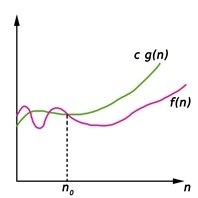
We write f(n) = O(g(n)), If there are positive constantsn0  and c such that, to the right of n0 the f(n) always lies on or below c*g(n).

O(g(n)) = { f(n) : There exist positive constant c and n0 such that 0 ≤ f(n) ≤ c g(n), for all n ≥ n0}

Big Omega Notation

Big-Omega (Ω) notation gives a lower bound for a function f(n) to within a constant factor.

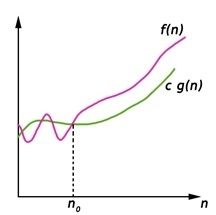
We write f(n) = Ω(g(n)), If there are positive constantsn0  and c such that, to the right of n0 the f(n) always lies on or above c*g(n).

Ω(g(n)) = { f(n) : There exist positive constant c and n0 such that 0 ≤ c g(n) ≤ f(n), for all n ≥ n0}

Big Theta Notation

Big-Theta(Θ) notation gives bound for a function f(n) to within a constant factor.

We write f(n) = Θ(g(n)), If there are positive constantsn0  and c1 and c2 such that, to the right of n0 the f(n) always lies between c1*g(n) and c2*g(n) inclusive.

 Θ(g(n)) = {f(n) : There exist positive constant c1, c2 and n0 such that 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n), for all n ≥ n0}

Properties:

1. Reflexivity:
If f(n) is given then

f(n) = O(f(n))

Example:
If f(n) = n³ ⇒ O(n³)
Similarly,

f(n) = Ω(f(n)) 
f(n) = Θ(f(n))

2. Symmetry:

f(n) = Θ(g(n)) if and only if g(n) = Θ(f(n))

Example:
If f(n) = n² and g(n) = n² then f(n) = Θ(n²) and g(n) = Θ(n²)
Proof:

• Necessary part:
  f(n) = Θ(g(n)) ⇒ g(n) = Θ(f(n))
  By the definition of Θ, there exists positive constants c1, c2, no such that c1.g(n) ≤ f(n) ≤ c2.g(n) for all n ≥ no
  ⇒ g(n) ≤ (1/c1).f(n) and g(n) ≥ (1/c2).f(n)
  ⇒ (1/c2).f(n) ≤ g(n) ≤ (1/c1).f(n)
  Since c1 and c2 are positive constants, 1/c1 and 1/c2 are well defined. Therefore, by the definition of Θ, g(n) = Θ(f(n))
• Sufficiency part:
  g(n) = Θ(f(n)) ⇒ f(n) = Θ(g(n))
  By the definition of Θ, there exists positive constants c1, c2, no such that c1.f(n) ≤ g(n) ≤ c2.f(n) for all n ≥ no
  ⇒ f(n) ≤ (1/c1).g(n) and f(n) ≥ (1/c2).g(n)
  ⇒ (1/c2).g(n) ≤ f(n) ≤ (1/c1).g(n)
  By the definition of Theta(Θ), f(n) = Θ(g(n))

3. Transistivity:

f(n) = O(g(n)) and g(n) = O(h(n)) ⇒ f(n) = O(h(n))

Example:
If f(n) = n, g(n) = n² and h(n) = n³
⇒ n is O(n²) and n² is O(n³) then n is O(n³)
Proof:
f(n) = O(g(n)) and g(n) = O(h(n)) ⇒ f(n) = O(h(n))
By the definition of Big-Oh(O), there exists positive constants c, no such that f(n) ≤ c.g(n) for all n ≥ no
⇒ f(n) ≤ c1.g(n)
⇒ g(n) ≤ c2.h(n)
⇒ f(n) ≤ c1.c2h(n)
⇒ f(n) ≤ c.h(n), where, c = c1.c2 By the definition, f(n) = O(h(n))
Similarly,

f(n) = Θ(g(n)) and g(n) = Θ(h(n)) ⇒ f(n) = Θ(h(n))
f(n) = Ω(g(n)) and g(n) = Ω(h(n)) ⇒ f(n) = Ω(h(n))
f(n) = o(g(n)) and g(n) = o(h(n)) ⇒ f(n) = o(h(n))
f(n) = ω(g(n)) and g(n) = ω(h(n)) ⇒ f(n) = ω(h(n))

4. Transpose Symmetry:

f(n) = O(g(n)) if and only if g(n) = Ω(f(n))

Example:
If f(n) = n and g(n) = n² then n is O(n²) and n² is Ω(n)
Proof:

• Necessary part:
  f(n) = O(g(n)) ⇒ g(n) = Ω(f(n))
  By the definition of Big-Oh (O) ⇒ f(n) ≤ c.g(n) for some positive constant c ⇒ g(n) ≥ (1/c).f(n)
  By the definition of Omega (Ω), g(n) = Ω(f(n))
• Sufficiency part:
  g(n) = Ω(f(n)) ⇒ f(n) = O(g(n))
  By the definition of Omega (Ω), for some positive constant c ⇒ g(n) ≥ c.f(n) ⇒ f(n) ≤ (1/c).g(n)
  By the definition of Big-Oh(O), f(n) = O(g(n))

Similarly,

f(n) = o(g(n)) if and only if g(n) = ω(f(n)) 

5. Since these properties hold for asymptotic notations, analogies can be drawn between functions f(n) and g(n) and two real numbers a and b.

• g(n) = O(f(n)) is similar to a ≤ b
• g(n) = Ω(f(n)) is similar to a ≥ b
• g(n) = Θ(f(n)) is similar to a = b
• g(n) = o(f(n)) is similar to a < b
• g(n) = ω(f(n)) is similar to a > b

6. Observations:

max(f(n), g(n)) = Θ(f(n) + g(n)) 

Proof:
Without loss of generality, assume f(n) ≤ g(n), ⇒ max(f(n), g(n)) = g(n)
Consider, g(n) ≤ max(f(n), g(n)) ≤ g(n)
⇒ g(n) ≤ max(f(n), g(n)) ≤ f(n) + g(n)
⇒ g(n)/2 + g(n)/2 ≤ max(f(n), g(n)) ≤ f(n) + g(n)
From what we assumed, we can write
⇒ f(n)/2 + g(n)/2 ≤ max(f(n), g(n)) ≤ f(n) + g(n)
⇒ (f(n) + g(n))/2 ≤ max(f(n), g(n)) ≤ f(n) + g(n)
By the definition of Θ, max(f(n), g(n)) = Θ(f(n) + g(n))

7. O(f(n)) + O(g(n)) = O(max(f(n), g(n)))

Proof:
Without loss of generality, assume f(n) ≤ g(n)
⇒ O(f(n)) + O(g(n)) = c1.f(n) + c2.g(n)
From what we assumed, we can write
O(f(n)) + O(g(n)) ≤ c1.g(n) + c2.g(n)
≤ (c1 + c2) g(n)
≤ c.g(n)
≤ c.max(f(n), g(n))
By the definition of Big-Oh(O),
O(f(n)) + O(g(n)) = O(max(f(n), g(n)))

Notes:

1. If lim _n→∞ f(n)/g(n) = c, c ∈ R+ then f(n) = Θ(g(n))
2. If lim _n→∞ f(n)/g(n) ≤ c, c ∈ R (c can be 0) then f(n) = O(g(n))
3. If lim _n→∞ f(n)/g(n) = 0, then f(n) = O(g(n)) and g(n) = O(f(n))
4. If lim _n→∞ f(n)/g(n) ≥ c, c ∈ R (c can be ∞) then f(n) = Ω(g(n))
5. If lim _n→∞ f(n)/g(n) = ∞, then f(n) = Ω(g(n))and g(n) = Ω(f(n))